Perfect Foreshortening

The construction of angular structures from points and edges taken from 3-views is standard practice, quite often even automated in modern drawing tools. Circles however seem to be too difficult. This page with its embedded calculator (needs javascript enabled!) shall help in such cases.

figure 1

Start by boxing the circle in the 3-view as shown in figure 1. Then transfer the box to the foreshortened view as in figure 2 and take the dimensions X,Y and H. Note that H needs to be taken at right angles to the longer box side Y, even if Y happens not to be vertical..

Put the three dimensions into the left hand column of the calculator below.

figure 2

Input Data

Length of Longer Box Side	Y	[units]
Length of Shorter Box Side	X	[units]
Orthogonal Width of Box	H	[units]

Results

Longer Axis	A	[units]
Shorter Axis	B	[units]
Bank Angle (left side)	w	[deg]
Bank Angle (right side)	w	[deg]

figure 3

Then draw a plain vanilla ellipse to the dimensions A and B (or tweak a circle if your tool supports this better) as shown in figure 3, turn it counterclockwise by angle w and move it into the box, aligning the centers of ellipse and box.

There are two possible values for w; the simple reason is that from the three input parameters the calculator can't tell whether the ellipse is to be used for the left or right side of a foreshortened object.

If Y happens not to be vertical, adjust w accordingly, as w is to be taken from H as the horizontal base.

The Math behind the Calculator

If you're just curious or even plan to build your own CAD system, read on...

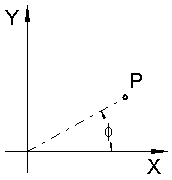
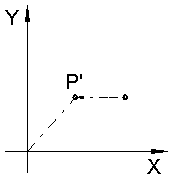
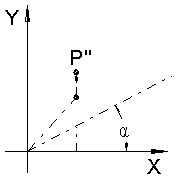
First of all the transformation from 3-view to foreshortened picture needs to be captured mathematically.

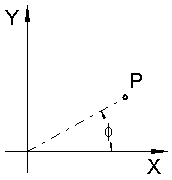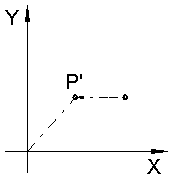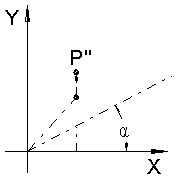In the 3-view we have a point P, given by its coordinates (x, y). The x coordinate is shortened (hence the name foreshortening?). Mathematically we formulate this by multiplying with a number z, which is less than 1.0. The new point P' is (z*x, y). And lastly the point is moved upward. Technically an auxiliary x-axis is drawn and the original y coordinate taken from there. Mathematically we calculate the offset from the x coordinate of P' and the angle α. So P" is (z*x, y + z*x*tan(α)).

Now let P be an element of a circle centered at (0,0) and with radius r:

(1) P(φ) = r*(cos(φ), sin(φ))

φ is a so called free parameter; think of it as denoting uniquely each point of the circle.
Doing our transformation as introduced above, we get:

(2) P"(φ) = r*(z*cos(φ), sin(φ) + z*tan(α)*cos(φ))

The distance K(φ) from (0,0) to P'' is easy to calculate using old friend Pythagoras (left as exercise for the reader ;-).

It is not unrealistic to expect some variation in K as we move φthrough a full period 0..360°. Especially there will be two maxima and two minima. To find them, we simply differentiate K with respect to φand look for the roots:

(3) dK/dφ = C(φ) * ((1 - z² * (tan²(α) + 1))*sin(2φ) + 2*z*tan(α)*cos(2φ)) = 0

If we ignore the term C(φ) (= 0.5 / K(φ), which will never become zero anyway), this collapses conveniently to

(4) tan(2φ) = 2*z*tan(α) / (z² * (tan²(α) + 1) - 1)

which has the required number of solutions, namely:

(5) Φ = { φ, φ+90°, φ+180°, φ+270° }

Now all we have to do is to calculate K(φ) and K(φ+90°) to get the two half-axis of the ellipse. Depending on size, we sort them into A and B. For the φ we used to get A, P'' is calculated and the angles w determined, conveniently using the atan2 function (if available):

(6)    A = 2*K(φ1)
(7)    B = 2*K(φ2)
(8)    wr = atan2(y"(φ1), x"(φ1))
(9)    wl = 90° - atan2(y"(φ1), x"(φ1))

Remains to define the geometric link to the user interface:

(10)    r = Y / 2
(11)    z = H / Y
(12)    cos(α) = H / X    =>    tan²(α) = X² / H² - 1


In the 3-view we have a point P, given by its coordinates (x, y).	The x coordinate is shortened (hence the name foreshortening?). Mathematically we formulate this by multiplying with a number z, which is less than 1.0. The new point P' is (z*x, y).	And lastly the point is moved upward. Technically an auxiliary x-axis is drawn and the original y coordinate taken from there. Mathematically we calculate the offset from the x coordinate of P' and the angle α. So P" is (zx, y + zx*tan(α)).