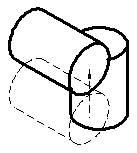
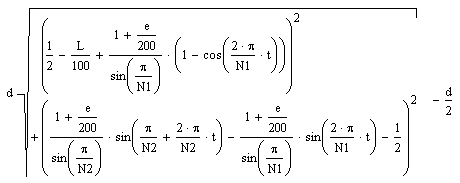 Relative to the green peg, the red peg as a whole just moves
up and down.
Relative to the green peg, the red peg as a whole just moves
up and down.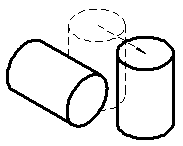 Relative to the red peg, the green peg primarily moves back and
forth.
Relative to the red peg, the green peg primarily moves back and
forth. 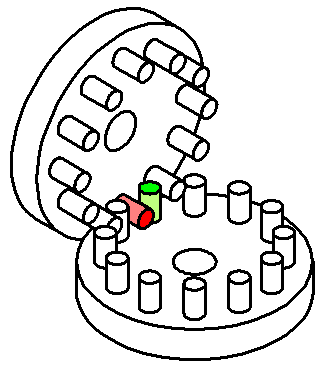 While building of such gear wheels is easy, the correct dimensioning
seems to be some black magic; to lift the veil a bit the following
text hopefully will provide enough understanding to get them first
time right in your next project.
While building of such gear wheels is easy, the correct dimensioning
seems to be some black magic; to lift the veil a bit the following
text hopefully will provide enough understanding to get them first
time right in your next project. Relative to the green peg, the red peg as a whole just moves
up and down.
Relative to the green peg, the red peg as a whole just moves
up and down. |
|
 Relative to the red peg, the green peg primarily moves back and
forth.
Relative to the red peg, the green peg primarily moves back and
forth. |
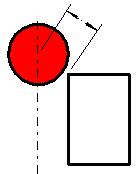
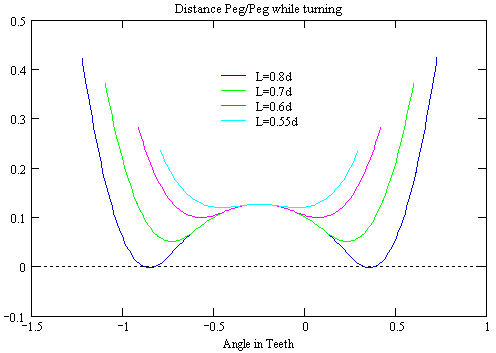
If the center of the red peg is above the top of the green peg, the pegs will not intersect if in the projection onto the vertical plane (front view) the distance between the center of the red peg and any corner of the green peg is longer than half the diameter of one peg. |
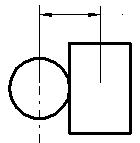
The pegs will not intersect as long as the horizontal distance of their centers is longer than their diameter. |
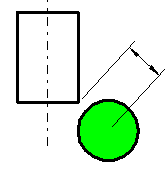
If the center of the green peg is in front of the front of the red peg, the pegs will not intersect if in the projection onto the horizontal plane (top view) the distance between the center of the green peg and any corner of the red peg is longer than half the diameter of one peg. |
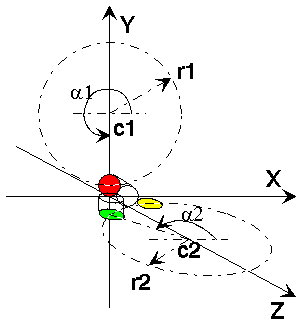 The fundamental idea behind all kinds of gearing is the equivalence
between two ratios: The ratio of the numbers of teeth is inversely proportional
to the number of turns for every pair of meshing gears. Using this rule,
the coordinate system shown right and looking at the pitch circles (the
circle the centers of the pegs are located on), we can write down the
equations for each peg:
The fundamental idea behind all kinds of gearing is the equivalence
between two ratios: The ratio of the numbers of teeth is inversely proportional
to the number of turns for every pair of meshing gears. Using this rule,
the coordinate system shown right and looking at the pitch circles (the
circle the centers of the pegs are located on), we can write down the
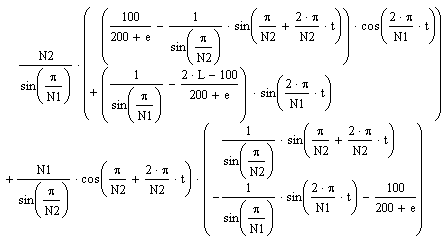
equations for each peg: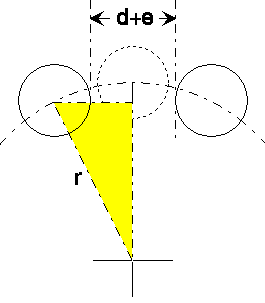 The pitch circle radius (r) is also determined by the number (n)
and diameter of the pegs:
The pitch circle radius (r) is also determined by the number (n)
and diameter of the pegs: