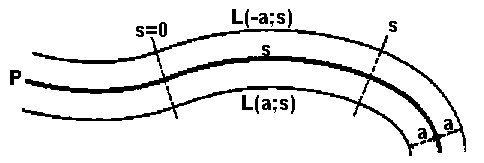Consider the figure to the right.
P denotes the path taken by the center of the
chariot, e.g. the base of the pointer's pole. The parallel
lines are the tracks of the road wheels, by design always holding a
distance (perpendicular to P) of
a, which is half the track width. For each
distance s traveled on the path P
the distance L as function of s
and distance a can be given. If the plane
isn't flat, a must be reasonable small to make
the following math valid. Next let's define q
as the angle turned by the pointer relative to some fixed point on
the chariot. Again we may assume that q is a
function of s. Now we postulate a design a valid
SPC construction if it fulfills the basic equation q(s) = {L(a;s) -
L(-a,s)} / 2a [q
measured in radian]That simple ? Let L(-a;s) be 0, i.e. the left wheel doesn't turn at all. If the chariot runs a full circle, L(a,s) will be 2*(2a)*PI for geometrical reasons (circumference of circle), whereas q(s) has to be one turn, that's 2*PI. Inserted in the equation, equality results. Q.E.D.
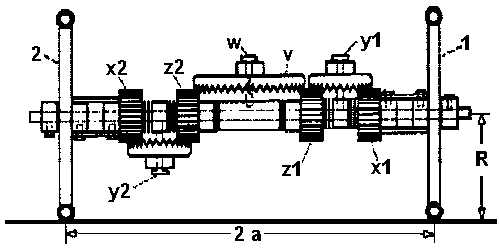As an example lets take the design of N. C.
Ta'Bois. The only things fixed to the horizontal shaft are the
shafts for the gears y1 and y2.
The shaft w (and the pointer) is held
vertical by the pole (not shown here, see picture of model).
Each wheel of radius R transforms the length
L along its track into a rotational angle for its
gear x
rot(x) = L(a;s) / RIf the horizontal shaft rotates at rot(h), the standard equation for differentials gives
rot(z) = 2*rot(h) - rot(x)The vertical shaft w does not rotate around the horizontal shaft. Therefore with the same differential formula
2 * rot(w) = rot(z1) + rot(z2)Next we take from the design that v has twice as many teeth as x, so we may state for the pointer
= 2*rot(h1) - rot(x1) + 2*rot(h2) - rot(x2) = 4*rot(h) - {rot(x1) + rot(x2)} = 02* rot(h) = {rot(x1) + rot(x2)} / 2
rot(v) = rot(z1) / 2All of this packed into the basic equation from the beginning of this chapter delivers:
q(s) = rot(v)The last two lines can be simplified to the wanted equation:= {2*rot(h) - rot(x1)} / 2= {L(a;s) - L(-a,s)} / 4*R
= {rot(x1) + rot(x2)} / 4 - rot(x1) / 2
= {rot(x2) - rot(x1)}/4
= {L(a;s) - L(-a,s)} / 2*a
R = a / 2Q.E.D.
