Understanding Planetary Gears

If You have mastered the basic gear calculus the next step is gears inside each other. A neat entry is shown in the figure below:
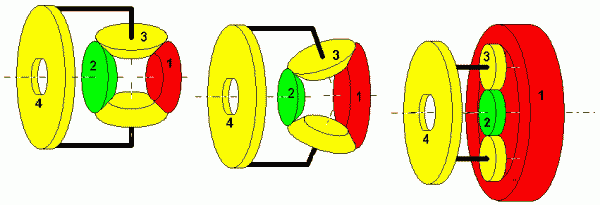
differential to planetary gear

To the left You see a standard differential. If you change the size of the left and right wheels the axles of the spider wheels must be angled to keep all wheels in contact, as shown in the middle. Continuing this process will ultimately give the configuration to the right:

The red part (1) is no longer a classical gear but an Annulus with the teeth pointing inward.
The green central wheel (2) is called the Sun wheel, probably because all the other wheels rotate around it as do the planets around our celestrial sun.
The yellow wheels (3) are called the Planet gears. Their number varies depending on load requirements; I've seen two to six, with a majority at three.
The Planet Carrier (4) finally cares for the proper alignment of the planets.

The math can be derived by some easy mental exercises.
First of all the gear sizes can't be chosen independently. As the planets touch all other parts a common tooth standard is required. And as number of teeth and diameter are proportional to each other the simple fact that all wheels have to stay in contact results in

	d₁ = d₂ + 2 * d₃
(1)	n₁ - n₂ = 2 * n₃

For the first exercise we hold the Planet Carrier fixed and take a POV from the left. Sun and Planet now are a simple pair of spur wheels. But Planet and Annulus always turn in the same direction because of the Annulus' teeth being on the far side of the Planet's axle, seen from the center of the Annulus. We get the equations for rot₄ = 0

	n₂ * rot₂ + n₃ * rot₃ = 0
	n₃ * rot₃ - n₁ * rot₁ = 0
(2)	n₂ * rot₂ + n₁ * rot₁ = 0
	rot₁ = - (n₂ / n₁) * rot₂
	rot₂ = - (n₁ / n₂) * rot₁

In the first execise we (the observer) sat at a place where the Planet Carrier was at rest. The Sun wheel turned in one direction, the Annulus in the opposite one.
Now lets take a seat on the Annulus. From this place the Planet Carrier turns in the same direction as the Sun wheel, but at a rate of -rot₁. The Sun wheel however turns relatively faster than before, namely with rot₂ - rot₁. Putting all together we get the equations for rot₁ = 0

	rot₄ = -rot₁
	rot₂ = -(n₁ / n₂) * rot₁ - rot₁
(3)	rot₂ = (1 + n₁ / n₂) * rot₄
	n₂ * rot₂ = (n₂ + n₁) * rot₄

The same exercise can be done with the sun wheel being at rest (rot₂ = 0)

	rot₄ = -rot₂
	rot₁ = -(n₂ / n₁) * rot₂ - rot₂
(4)	rot₁ = (1 + n₂ / n₁) * rot₄
	n₁ * rot₁ = (n₁ + n₂) * rot₄

Summing all this up we get the Universal Equation for Planetary Gears:

(5)	n₁ * rot₁ + n₂ * rot₂ = (n₁ + n₂) * rot₄